

Wiadomości przeciętnego chemika o pH są następujące:
- wielkość ta została
wprowadzona przez Sorensena
dla uproszczenia obliczeń i zapisów
- pH jest to ujemny logarytm
ze stężenia jonów wodorowych (oksoniowych)
- pH jest miarą kwasowości
roztworu
- pH roztworu obojętnego
(neutralnego), równe jest 7,00
Niestety, tezy te są prawdziwe zaledwie w „pewnym stopniu”.
Po co
Sorensen to zrobił?
Jest zastanawiające, że w
ciągu wielu lat zajęć dydaktycznych żaden ze Studentów nie zadał mi tego
pytania... Gdyby jednak ogłoszono w prasie, że od jutra w handlu dozwolone
będzie stosowanie jedynie logarytmów z
kilogramów np. kartofli, w miejsce dotychczasowych kilogramów, wywołałoby
to powszechne protesty i pytania. Wielkości logarytmiczne wprowadzono
pierwotnie rzeczywiście po to, aby uprościć zapis iloczynu potęgowego np.
zamiast 3,8x10-5; -4,42 - w skali logarytmicznej. Drugim celem było
„spłaszczenie” rozpiętości skali. Stężenie jonów wodorowych rozciąga się od
wartości 10-14 (który Czytelnik potrafi nazwać tę liczbę?) w 1M
roztworze NaOH, do jedności w 1M HCl. Użycie nieliniowej skali logarytmicznej
ma podobny cel, jak obrazowanie np. historii Ziemi w logarytmicznej skali
czasowej. Powoduje to „skrócenie” bardzo odległych okresów, (w których zmiany
były bardzo powolne) i rozciągnięcie skali nieodległej przeszłości, w której
zachodziły gwałtowne zmiany. Z logarytmicznych właściwości skali pH chemicy
muszą jednak zdawać sobie sprawę. Jeżeli np. podczas miareczkowania, dodatek 1
kropli powoduje zmianę pH o 5 jednostek, to odpowiada temu zmiana stężenia
jonów wodorowych 100 000 razy! Jest więc dyskusyjne, czy wprowadzenie
logarytmicznej jednostki stężenia, jest rzeczywistym uproszczeniem, szczególnie
gdy zważyć powszechną niechęć do logarytmów...
Symbol „p” jednostki pH pochodzi od łacińskiego: potentio = potęga (tu: jej wykładnik ze
zmienionym znakiem).
Pochwała
logarytmów
Odnoszę wrażenie że
początkujący chemicy traktują logarytmy jako złośliwą represję. Trzeba więc
przypomnieć, że wynalazek logarytmów pojawił się w XVII w. i był podyktowany
praktyczną koniecznością ułatwienia niezwykle żmudnych obliczeń, które
ówczesnym astronomom pochłaniały znaczną część życia. Znakomity opis
konstruowania tablic logarytmicznych można znaleźć w cytowanej literaturze.
Innym praktycznym zastosowaniem logarytmów był suwak logarytmiczny - proste
urządzenie służące do wykonywania szybkich obliczeń w technice. Współczesny
kalkulator w rękach Studentów zdaje się jednak służyć przede wszystkim do
odzwyczajania ich od myślenia matematycznego. Przeciętny Student poproszony o
obliczenie np.: 30 x 0,2 - z reguły
sięga machinalnie po kalkulator! W okresie używania suwaków logarytmicznych
podobna sytuacja była wręcz nie do pomyślenia... Czy na tym ma polegać
pokoleniowy postęp techniczny i intelektualny?
Suwak logarytmiczny
przeszedł swego rodzaju „nobilitację” podczas projektowania konstrukcji bomby
wodorowej w „Projekcie Manhattan”. Zespół kilku przeszkolonych sekretarek
wykonał ciąg kontrolnych obliczeń za pomocą suwaków logarytmicznych szybciej,
niż zdołano to zrobić używając maszyny elektronicznej „MANIAC”! Znajomość
właściwości logarytmów (a nie tylko umiejętność naciskania klawisza kalkulatora
posiadającego funkcję logarytmiczną!) jest niezbędna do zrozumienia niektórych
zależności spotykanych w życiu codziennym.
Loga-rytmiczna muzyka
Prawo Webera-Fechnera
opisuje zależność pomiędzy subiektywnym wrażeniem fizjologicznym (np. głośność, słoność, jasność), a fizyczną
wartością działającego bodźca. Wrażenie fizjologiczne jest proporcjonalne do logarytmu z wielkości bodźca. Ta
szczególna właściwość mózgu jest prawdopodobnie zabezpieczeniem przed
nadmiernym dopływem bodźców z otoczenia. A więc np. dwukrotne zwiększenie mocy
wzmacniacza powoduje wzrost głośności muzyki 1,3 raza. Rachunek: log 2 = 0,3, a
zatem nowa głośność wynosi: 1 + 0,3 = 1,3 raza (w podobny sposób zdefiniowano
jednostki głośności - decybele). Młodzi pirotechnicy sądzą czasem, że
sporządzenie 10-krotnie większego ładunku wybuchowego, da w wyniku
proporcjonalnie większy huk. Jeśli znają oni prawo Webera-Fechnera, to nie będą
rozczarowani faktem, że dźwięk będzie zaledwie dwukrotnie silniejszy (natomiast zagrożenie skutkami mechanicznymi
wybuchu może być nawet wielokrotnie większe niż 10). Przy fotografowaniu zimą
bez światłomierza, przecenia się z reguły natężenie światła, co prowadzi do
niedoświetlenia zdjęć. Podobne zależności opisują prozaiczny proces brudzenia
się.
Dopiero później pojawiło się
najbardziej sensowne uzasadnienie stosowania skali pH. Niektóre z fizykochemicznych
wielkości (np. potencjał elektrody) zależą od stężenia kwasu. Zależność ta ma
skomplikowaną wykładniczą postać algebraiczną. Zastąpienie stężenia jonów
wodorowych wielkością pH, upraszcza znacznie tę zależność: E = A
– 0,059 pH. Jest zaskakujące, że elektrody o zupełnie różnej budowie: wodorowa, antymonowa, chinhydronowa, szklana
– wykazują identyczną prostą zależność liniową.
Wymiar jednostki pH
Z
reguły przyjmuje się, że jednostka pH jest bezwymiarowa... Wartość liczbowa pH
zależy od tego, czy stężenie (aktywność) wyrażone jest w np. molach na litr,
czy chociażby, jako stężenie procentowe. Zupełnie poprawnie, wymiarem pH
powinien być logarytm z wymiaru stężenia. Ponieważ przyjęto, że w chemii
jednostką stężenia jest stężenie molowe
(M = mol/l), zatem w praktyce problem ten jest nieistotny...
pH nie jest
miarą kwasowości...
Ujemny znak logarytmu w
definicji pH przyjęto pierwotnie dla uniknięcia operowania liczbami ujemnymi.
Niestety, zmieniło to sens tak sformułowanej wielkości. Im większe stężenie kwasu (i jonów wodorowych), tym niższe pH. pH jest więc raczej miarą zasadowości niż kwasowości roztworu! To
pomieszanie pojęć można zauważyć w wielu podręcznikach chemii analitycznej.
Wykresy zmian pH rysowane są często „do góry nogami”. Jest to drobny, ale
irytujący błąd; strzałka na osi „pH” wskazuje bowiem kierunek wzrastania
opisanych na osi wartości liczbowych. Autorzy podręczników chemii analitycznej
mają na sumieniu błędy o wiele poważniejsze, jak chociażby sformułowanie: „w obecności fenoloftaleiny zmiareczkowaniu
kwasem ulega połowa Na2CO3”.
W trudnych latach 50-tych niektórzy
autorzy nie wahali się przed dodawaniem komentarzy ideowo-politycznych,
niewiele mających wspólnego z chemią. Reakcję zobojętnienia przedstawiono
jako... przykład marksistowskiego prawa walki i jedności przeciwieństw! „W ten sposób pojęcia jakby przeciwstawne –
kwas i zasada – są połączone w jednym pojęciu – stężenia jonów wodorowych. Jest
to jeden z licznych przykładów ogólnego prawa jedności i walki przeciwieństw.W
myśl tego prawa wszystkim przedmiotom w przyrodzie właściwe są wewnętrzne
sprzeczności, albowiem wszystkie one mają swą stronę dodatnią i ujemną, przy
czym obie te strony są równie nierozdzielne, jak przeciwstawne”. Niech ten
cytat będzie raczej próbą przybliżenia atmosfery tamtych czasów, niż
przyczynkiem do poznania dialektycznej mentalności autora fragmentu...
O całkowitym niezrozumieniu
znaczenia jednostki pH świadczy treść telewizyjnej reklamy pewnej pasty do
zębów: „likwiduje pH w ustach!”. Podobny sens ma nawoływanie do
„pozbycia się wszystkich substancji
chemicznych z naszego otoczenia”.
Roztwór obojętny: pH = 6,85
W roztworze obojętnym
(„neutralnym”) pH jest identyczne jak w czystej# wodzie. W czystej
# „czystej” nie oznacza wziętej z butli „woda destylowana”, stojącej w laboratorium. Taka woda zawiera nieznaczne ilości CO2 pochłoniętego z powietrza, który nadaje jej pH 4-5.
wodzie stężenie jonów wodorowych równe jest pierwiastkowi z iloczynu jonowego wody. Ale wartość liczbowa iloczynu jonowego wody nie jest równa dokładnie 10-14. Poza tym zależy ona zarówno od mocy jonowej roztworu, jak i temperatury. Jeśli zatem w pewnych warunkach wartość iloczynu jonowego wody wyniesie 2x10-14, to stężenie jonów wodorowych równe będzie ok. 1,41x10-7, a w konsekwencji pH takiego (obojętnego!) roztworu, wynosić będzie 6,85. W temperaturze 80oC wartość iloczynu jonowego wody równa jest ok. 10-13. Ile wynosi pH neutralnego roztworu w tych warunkach? Jest interesujące, czy układ kompensujący zmiany temperatury, wmontowany w droższych modelach pH-metrów, uwzględnia tylko wpływ temperatury na wartość stałych w równaniu Nernsta, czy także uwzględnia zmienność wartości iloczynu jonowego wody? Również obecność obojętnych soli powoduje wzrost wartości Kw - na skutek efektu solnego. Zupełnie poprawnie: roztwór obojętny (neutralny) należy zdefiniować jako roztwór, w którym stężenia jonów wodorowych i jonów wodorotlenkowych są sobie równe. pH takiego neutralnego roztworu może więc być różne od 7,00.
Aktywność zamiast stężenia. Bulwersująca definicja pH
Wkrótce po sformułowaniu
teorii mocnych elektrolitów trzeba było zmodyfikować definicję pH: jest to
ujemny logarytm z aktywności jonów
wodorowych (oksoniowych). Ta drobna zmiana spowodowała jednak istotne
konsekwencje. Współczynniki aktywności zależą bowiem m.in. od mocy jonowej
roztworu. Równania które opisują tę zależność mają jednak tylko przybliżony,
empiryczny charakter. Ponieważ aktywności nie da się dokładnie obliczyć, zatem
również nie da się dokładnie obliczyć wartości pH! Powszechnie znany wzór z
logarytmem jest zaledwie przybliżonym sposobem oszacowania pH. Wobec tych trudności, IUPAC wprowadził oficjalną definicję pH, która zapewne będzie
zupełnym zaskoczeniem dla wielu chemików:
pH jest to odczyt ze skali pH-metru, którego elektrody zanurzone są w badanym roztworze. pH-metr uprzednio powinien być wykalibrowany przy użyciu międzynarodowych wzorcowych roztworów buforowych.
Próby obliczeń pH, w sposób taki jak dzieje się w programie studiów, obarczone są często wielkimi błędami. Powodem jest zarówno niemożność właściwego obliczenia współczynników aktywności, jak i pominięcie faktu niecałkowitej dysocjacji kwasów i soli, a wreszcie pominięcie innych równowag protolitycznych w roztworze. Takie obliczenia prowadzą do różnicy pH już na pierwszym miejscu dziesiętnym po przecinku. Można to łatwo sprawdzić obliczając pH jakiegokolwiek roztworu buforowego podawanego w którymś z poradników chemicznych, i porównując wynik z wartością pH podaną obok tego przepisu. W takiej sytuacji należy mieć zaufanie do poradnika, a nie do ułomnych obliczeń. Niektórzy wykładowcy żądają jednak podawania przez Studentów wyników obliczeń pH z dokładnością do 0,001 pH. Prawdopodobnie nie mieli oni nigdy do czynienia z rzeczywistymi pomiarami potencjometrycznymi pH... Nieco inaczej przedstawia się problem doświadczalnych pomiarów pH realnych roztworów. W tym przypadku dokładność limitowana jest głównie jakością przyrządu oraz rzetelnością wzorcowych buforów; z reguły nie przekracza ona 0,01 jednostki pH.
Wirtualna chemia
Rysunki „eleganckich”
krzywych miareczkowania zamieszczanych w podręcznikach obliczane są w bardzo
uproszczony sposób i dlatego rzeczywisty przebieg zmian podczas miareczkowania
może być przykrym zaskoczeniem dla eksperymentatora. Kolejny raz pojawia się
więc problem dydaktyczny: jak głęboko należy wdawać się w rzeczywisty opis
zjawisk przyrodniczych? Co powinno być wyróżnikiem: rzetelność czy poglądowość
i chęć uniknięcia niepotrzebnego zamieszania? Niewątpliwie decyduje o tym poziom
audytorium i intuicja wykładowcy...
Uproszczony sposób opisu
rzeczywistości jest kuszący ze względu na swą poglądowość. Coraz częściej
spotykamy się z ludźmi zafascynowanymi takim wirtualnym obrazem. Rosną również
naciski na wprowadzanie w miejsce kosztownych i uciążliwych zajęć
laboratoryjnych – odpowiednich symulacji komputerowych... Niestety, tendencje
te mają wspólną cechę: jest nią niebezpieczeństwo stworzenia nierzeczywistego,
uproszczonego obrazu otaczającego nas świata. Urok chemii polega m.in. na nie
dających się z góry przewidzieć niespodziankach: takich jak np. pętla histerezy
podczas miareczkowań w układzie: CO2 – NaHCO3 – Na2CO3,
niezwykły kinetycznie przebieg zobojętnienia roztworu CO2 oraz
niezliczona liczba procesów, których zaskakujący przebieg odkryto najpierw
doświadczalnie, a dopiero potem żmudnie konstruowano opis teoretyczny. Ta
sytuacja zresztą trwa do dziś i jest jednym z motorów postępu wiedzy. W
momencie, w którym wszystko w chemii da się przewidzieć dokonując odpowiednich
obliczeń, chemia straci wiele ze swego uroku... Jaki sens mają więc zaoczne
studia chemiczne lub projekt telewizyjnych lub internetowych studiów
chemicznych? W znacznym stopniu jedynie wirtualny...
Nie można jednak przemilczeć faktu, że coraz częściej niektóre zjawiska i
rozwiązania chemiczne dają się przewidzieć lub zaprojektować teoretycznie.
Propozycje
innych jednostek...
Opisane niedogodności
związane z jednostką wprowadzoną (trzeba przyznać: dość pochopnie) przez
Sorensena były powodem, dla
którego zaproponowano wiele innych wielkości zamiast jednostki pH. Większość
tych sugestii sprowadza się do przywrócenia proporcjonalności do stężenia
kwasu; z reguły pozostawia się logarytmiczny charakter nowych jednostek.
Jedynie niektóre propozycje wracają do liniowej (nielogarytmicznej) zależności
od stężenia. Tylko propozycja A.G. uwzględnia fakt zmienności wartości
liczbowej iloczynu jonowego wody. Żadna z nich nie doczekała się jednak
praktycznego zastosowania, podobnie zresztą jak wielkość pOH. Pomimo wszystkich
niedogodności jednostki pH podanej przez Sorensena w 1909 roku, będzie ona zapewne jeszcze
długo powszechnie stosowana.
Niektóre
z propozycji są następujące :
pOH
= 14 – pH
XH
= 7 – pH
cH = 16 – pH![]() (A.G. = acidity grade, stopień kwasowości) A.G. = 14 – 2 pH
(A.G. = acidity grade, stopień kwasowości) A.G. = 14 – 2 pH
S.A.
= [H+] x 107 (S.A.
= scale of acidity)
Do większości z nich stosują się zastrzeżenia podobne, jak do jednostki pH
|
|
funkcja: |
jest miarą: |
wartość w środowisku: |
||
|
zasadowym |
neutralnym |
kwasowym |
|||
|
pH |
logarytmiczna |
zasadowości |
> 7 |
ok. 7 |
< 7 |
|
pOH |
logarytmiczna |
kwasowości |
< 7 |
ok. 7 |
> 7 |
|
XH |
logarytmiczna |
kwasowości |
ujemna |
ok. 0 |
dodatnia |
|
cH |
logarytmiczna |
kwasowości |
< 9 |
ok. 9 |
9 – 16 |
|
A.G. |
logarytmiczna |
kwasowości |
ujemna |
= 0 |
dodatnia |
|
S.A. |
liniowa |
kwasowości |
0 – 1 |
ok. 1 |
>1 |
Koniec z
miareczkowaniami?
Praktyczne wykonanie pomiaru
pH jest bardzo proste: do roztworu wstawia się elektrody i wynik pomiaru
odczytuje ze skali pH-metru. Ponieważ pH jest właściwie wielkością stężenia
jonów wodorowych - czy zatem zamiast żmudnego miareczkowania: sporządzania i
mianowania roztworów roboczych i kłopotliwego miareczkowania, nie wystarczy
zmierzyć wartość pH roztworu i obliczyć stężenie kwasu?
Dla
bardzo rozcieńczonych roztworów (woda deszczowa lub próbki ścieków), istotnie,
zamiast stężenia jonów wodorowych, podaje się często wartość pH. Dla roztworów
bardziej stężonych w taki sposób można obliczyć jedynie aktywność jonów wodorowych, natomiast obliczenie stężenia kwasu jest niemożliwe na
skutek znacznego błędu empirycznych równań opisujących współczynniki
aktywności. Błąd odczytu 0,01 pH odpowiada błędowi 2% w przeliczeniu na
aktywność jonów wodorowych. Do tego dochodzi błąd samego pomiaru pH oraz błąd
roztworów wzorcowych. Można przyjąć, że sumaryczny błąd wyznaczenia stężenia
jonów wodorowych na podstawie pojedynczego pomiaru
pH, jest nie mniejszy od 10%. Natomiast osiągalna praktycznie dokładność
miareczkowania alkacymetrycznego, sięga 0,1%; jest to więc dokładność 100 razy
większa! Nieprędko zatem zrezygnujemy z miareczkowania...
Podczas alkacymetrycznego
miareczkowania potencjometrycznego mierzone są co prawda wartości pH, służą one
jednak tylko do wyznaczenia punktu równoważnikowego. Stężenie próbki obliczane
jest z rachunku stechiometrycznego reagentów, a nie na podstawie odczytanej wartości
pH w P.R. Na podstawie wartości pH w P.R. można natomiast wyliczyć wartość
liczbową stałej dysocjacji
miareczkowanego słabego kwasu. Ponieważ jednak krzywa miareczkowania w pobliżu
P.R. jest bardzo stroma, wynik obliczeń obarczony jest znacznym błędem.
Dokładniejszy rezultat daje obliczenie pKa
na podstawie wartości pH zmierzonej w 50% zobojętnienia (pKa słabego kwasu równa jest po prostu zmierzonej w takim
momencie wartości pH. I to niezależnie od stężeń reagentów). Równie dokładne
wyniki uzyskuje się z pomiarów spektrokolorymetrycznych.
Skala pH: od
+47 do -33? (żart)
W miarę rozcieńczania
roztworu HCl, pH tego roztworu rośnie... Jaka jest zatem największa wartość pH?
Odpowiada ona najmniejszej ilości HCl rozpuszczonej w największej możliwej ilości
wody. Najmniejszą ilością HCl jest jedna cząsteczka HCl (ok. 1,7x10-24
mola). Całkowitą ilość wody dostępną na Ziemi szacuje się na 1023
litrów. Stężenie HCl wyniesie więc ok. 10-47 M. Stąd: pH = 47 (HCl
jest całkowicie zdysocjowany w tych warunkach). Zupełnie podobnie: najmniejsze
stężenie NaOH (oraz jonów OH-) wynosi 10-47 M, a więc
stężenie jonów wodorowych obliczone z iloczynu jonowego wody, równe jest 1033
M. Stąd rozpiętość skali pH: od +47 do
-33!
Czytelnik, który pamięta o
dysocjacji wody, łatwo wskaże błąd w tym rozumowaniu. Stężenie HCl (tzw.
„stężenie analityczne”) może co prawda maleć do zera, natomiast stężenie jonów
wodorowych w wodnym roztworze kwasu
nigdy nie może być mniejsze niż ok. 10-7 M. Przez rozcieńczanie
kwasu solnego nigdy przecież nie otrzyma się roztworu zasadowego!
Inna wersja postawionego zadania polega na uzupełnieniu prostej tabeli i wskazaniu przyczyny absurdalnego wyniku w ostatnim wierszu:
|
CHCl |
[H+] |
pH |
| 1 = 100 | 1 = 100 | 0 |
| 0,1 = 10-1 | 10-1 | 1 |
| 0,01 = 10-2 | 10-2 | 2 |
| 0,001 = 10-3 | 10-3 | 3 |
| ...... | ...... | ...... |
| ...... | ...... | ...... |
| 10-14 | 10-14 | 14 (???) |
Błąd polega na tym, że w środkowej rubryce: [H+] powinno być sumą stężeń jonów wodorowych pochodzących z dysocjacji kwasu oraz z dysocjacji wody. Dla dość stężonych roztworów można pominąć udział dysocjacji wody. Natomiast dla roztworów bardzo rozcieńczonych (dolna część tabeli), udział dysocjacji wody jest decydujący!
Pożyteczne jest przedstawienie wykresu obrazującego zależność całkowitego stężenia jonów wodorowych [H+] od stężenia analitycznego HCl. Wykres po prawej stronie jest bardzo znacznym powiększeniem fragmentu zależności, w zakresie skrajnie małych stężeń (a więc dla bardzo rozcieńczonego roztworu kwasu).
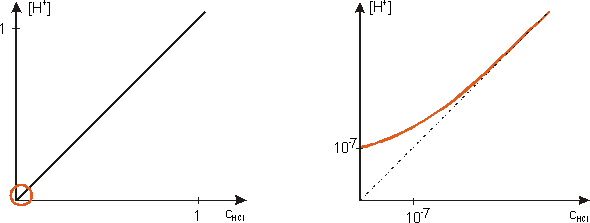
Całkowite stężenie jonów H+ jest sumą stężeń jonów wodorowych pochodzących z (całkowitej) dysocjacji kwasu, oraz z (nieznacznej) dysocjacji wody. Ponieważ dysocjacja wody zostaje cofnięta na skutek dodania kwasu, zatem suma jest dość zawiłą funkcją nieliniową. W zakresie znacznych stężeń kwasu udział dysocjacji wody można pominąć. Natomiast dla stężeń kwasu rzędu 10-7 i mniejszych, udział jonów pochodzących z dysocjacji wody jest decydujący.
Kontynuując poważne rozważania, najmniejsza możliwa wartość pH określona jest przez największe możliwe stężenie kwasu. W tak stężonych roztworach nie ma jednak żadnej możliwości chociażby oszacowania przybliżonej wartości pH na podstawie stężenia kwasu. Trzeba zdać się na praktyczny pomiar pH-metrem. Doświadczenie wskazuje, że odpowiednio stężone roztwory mocnych kwasów mają pH wyraźnie mniejsze od zera. Analogiczne pomiary stężonych roztworów mocnych zasad są trudniejsze do przeprowadzenia ze względu na specyficzną właściwość szklanej elektrody pomiarowej, tzw. „błąd sodowy” - i możliwość jej nieodwracalnego uszkodzenia.
Prawo Ostwalda
Prawo
Ostwalda opisuje zależność algebraiczną pomiędzy: stopniem (procentem)
dysocjacji α, stałą dysocjacji K
i stężeniem („analitycznym”) c słabego
elektrolitu binarnego (czyli typu AB. Dla innych substancji zależności są
bardziej skomplikowane):
![]() (1) cα2 + Kα – K
= 0 K = const. (1a)
(1) cα2 + Kα – K
= 0 K = const. (1a)
Konsekwencją tego równania jest zależność stopnia (procentu) dysocjacji – od rozcieńczenia. Dla uproszczenia obliczeń stosuje się często przybliżoną postać:
![]() (2)
(2)
Można łatwo sprawdzić, że dla bardzo rozcieńczonych roztworów niezbyt
słabych elektrolitów, stopień dysocjacji obliczony w taki sposób,
przekracza wartość „1”, czyli 100%! W takim przypadku nie wolno oczywiście
stosować przybliżonego równania (2).
Ponieważ stopień (procent)
dysocjacji zmienia się wraz z rozcieńczeniem, zatem nie jest on odpowiednim
kryterium do klasyfikacji mocy elektrolitów. Wielkością taką jest natomiast stała dysocjacji. Umownie przyjmuje
się, że substancje których stała dysocjacji jest mniejsza niż 10-3,
określane są jako słabe elektrolity. W niektórych podręcznikach szkolnych
ciągle można znaleźć jednak informację, że słabe elektrolity są to substancje,
które dysocjują w niewielkim (np. 5%) stopniu.
Dla wodnych roztworów elektrolitów będących słabymi kwasamilub zasadami obowiązują
jeszcze inne ograniczenia. Z równania (1)
wynika, że stopień (procent) dysocjacji w miarę rozcieńczania do
nieskończoności, powinien rosnąć do 100%. Pomimo tego substancja ta zaliczana
jest ciągle do słabych elektrolitów.
W mowie potocznej moc mylona jest
powszechnie ze stężeniem. I tak np.
5-procentowy ocet nazywany jest jako „słaby”,
w odróżnieniu od 10-procentowego („mocnego”),
nie mówiąc już o 70-procentowej „esencji octowej”, która określana jest jako
wręcz „żrąca”. Chemicy pod pojęciem mocy rozumieją więc zupełnie inną
właściwość.
Dla słabego kwasu o stałej dysocjacji Ka, zdysocjowanego w stopniu α , postarajmy się pozbyć w równaniu (1) jawnej zależności od stężenia c, a pozostawić zależność od stężenia jonów wodorowych [H+]:
![]() (3)
(3)
Należy pamiętać, że stężenie jonów wodorowych w nieskończenie rozcieńczonym roztworze kwasu jest takie samo jak w czystej wodzie, a więc równe jest ok. 10-7. W tych warunkach maksymalny (przy nieskończenie wielkim rozcieńczeniu) stopień (procent) dysocjacji słabego kwasu, wcale nie jest równy 100%, a wartość ta zależy od stałej dysocjacji:
![]() (4)
(4)
Dla kwasu o Ka = 10-7, maksymalny stopień dysocjacji wynosi 50%, dla kwasu o Ka = 10-8 maksymalny stopień dysocjacji wynosi tylko ok. 10%, a dla kwasu o Ka = 10-9, zaledwie 1%. Podobne zależności obowiązują dla wodnych roztworów słabych zasad.
Kwasowość i zasadowość wody, jonów oksoniowych i wodorotlenkowych
Przy porównywaniu wartości
stałych dysocjacji Ka
bardzo słabych kwasów, konfrontuje się je z wartością: 10-14 wody. Jest
to jednak wartość iloczynu jonowego
wody. Wartość Ka wody
wynosi:
H2O + H2O <=> H3O+ + OH-
![]() stąd:
pKa = 15,74
stąd:
pKa = 15,74
Identyczne wartości mają odpowiednie stałe zasadowości wody. Czytelnik zechce wykazać, że wartości: Ka dla kationu oksoniowego, oraz: Kb dla anionu wodorotlenkowego
H3O+ + H2O <=>
H2O + H3O+
OH- + H2O <=> H2O + OH-
wynoszą: 55,5, a więc odpowiednie wartości pK, równe są: -1,74.
LITERATURA
J.Chem.Educ., 71,
747 (1994). [„Uczyć prawdy o pH”]
J.Chem.Educ., 38, 365 (1961), 76, 892 (1999). [Propozycje innych jednostek]
J.Chem.Educ., 72, 954 (1995).
[Wymiar
jednostek logarytmicznych]
J.Chem.Educ., 49, 776 (1972).
[pH = 47 ?]
J.Chem.Educ., 38, 260 (1961).
[Stała
jonizacji wody]
J.Chem.Educ., 68, 304 (1991).
[Zasadowość
wody i OH- oraz kwasowość wody i H3O+]
R.P.Feynman, R.B.Leighton, M.Sands. „Feynmana
wykłady z fizyki. Tom I cz. I”. PWN, Warszawa 1971, s. 319. [Konstruowanie tablic logarytmicznych]
J.Aleksiejewski,
R.Golc, A.Musakin. „Analiza jakościowa”. PWN, Warszawa 1954, s. 283.
[Reakcja zobojętnienia jako przykład dialektyki]
S.H. Ulam, „Przygody matematyka”, Wyd. „Prószyński”, Warszawa 1998, s.242. [„Superbomba na suwaku”].
Tomasz Pluciński - tomek@chemik.chem.univ.gda.pl
Praca wpłynęła do ChemFana: 2000-06-02
