

Dobieranie współczynników w równaniach reakcji jest ulubionym ćwiczeniem zadawanym przez nauczycieli chemii w szkole, a również przez wykładowców uniwersytetu. Temu tematowi poświęcana jest nieproporcjonalnie wielka część programów nauczania. Wydaje się, że można ten czas spożytkować lepiej: na wyjaśnianie istotnych praktycznych problemów chemicznych. Gorzej, że wykładowcy preferują taki sposób zapisywania równań, który nie jest właściwy z merytorycznego punktu widzenia... Jeśli doświadczonego chemika poprosić o pomoc w zapisaniu nieco bardziej skomplikowanego, nietypowego równania, to z reguły próbuje on zastosować stopnie utlenienia. Po kilku bezskutecznych próbach oświadcza, że "zajmie się tym równaniem w domu"... po czym stosuje najbardziej typową dla chemików metodę: "na chybił-trafił". Wydaje się że postępuje tak większość nauczycieli chemii (w tym również akademickich). Ta najpopularniejsza metoda nie będzie tu omawiana. W czasopiśmie Journal of Chemical Education sformułowano wręcz kiedyś tezę, że to właśnie chemicy najczęściej zapisują równania reakcji chemicznych nieprawidłowo.
Poniższy tekst zawiera wiele kontrowersyjnych twierdzeń i krytycznych uwag dotyczących metod powszechnie stosowanych przez chemików. Niektóre z twierdzeń są tak paradoksalne, że doprowadziły autora w pewnym momencie do przyznania, że nie potrafi on zdefiniować reakcji utleniania-redukcji! Tekst ten nie jest więc przeznaczony dla osób uczestniczących w początkowym kursie chemii. Pomyślany jest jako prowokacja do dyskusji nad zasadnością typowych dla chemików sposobów zapisywania równań i jako zachęta do poznania innych, skuteczniejszych, a mało znanych procedur... Dodatkowo autor chciałby wykazać, że taki sposób potraktowania jednego z najnudniejszych działów chemii może być naprawdę zajmujący.
Powszechnie stosowane przez chemików procedury wyznaczania współczynników w równaniach reakcji utleniania-redukcji opierają się na stopniach utlenienia atomów.
STOPNIE UTLENIENIA I BILANS ELEKTRONOWY
Stopnie utlenienia są w gruncie rzeczy przydatne jedynie do celów klasyfikacji związków nieorganicznych, oraz - w jednej z procedur wyznaczania współczynników w
niektórych rodzajach równań reakcji chemicznych. Niestety, większość chemików nie wyobraża sobie chemii bez stopni utlenienia, a co gorsze, przypisuje stopniom utlenienia znaczenie, jakiego one nie mają. Są to wielkości umowne, które zależne są od sposobu ich obliczania... Atomom wodoru w cząsteczkach związków przypisuje się stopień utlenienia +1, jedynie w wodorkach metali alkalicznych wynosi on -1 (a jaki stopień utlenienia przyjąć w wodorkach pierwiastków przejściowych?). Atomom tlenu przypisuje się stopień utlenienia -2, za wyjątkiem atomów tlenu uczestniczących w wiązaniu nadtlenkowym -O-O- * (stopień utlenienia -1), ponadtlenkach np. KO2 (-1/2) oraz w fluorku tlenu* dlaczego nie potraktowano w tych regułach w identyczny sposób wielosiarczków?
F2O, gdzie wynosi on +2. Suma stopni utlenienia równa jest ładunkowi jonu (dla obojętnej cząsteczki wynosi zatem 0). Reguła ta nie sugeruje sposobu postępowania w przypadku bardziej skomplikowanych cząsteczek. Można więc przyjąć, że dopuszcza to pewną dowolność w takich przypadkach.
Opis metody należy zacząć od przytoczenia przykładu jej zastosowania. Wyznacza się wartości stopni utlenienia tych atomów, które ulegają zmianie podczas reakcji, a następnie oblicza się różnicę stopni utlenienia w wyniku reakcji. Różnica ta równa jest liczbie wymienianych elektronów. Bilanse przeprowadza się dla cząsteczek substratów w takiej postaci, w jakiej zapisane są po lewej stronie równania.
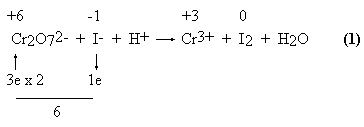
Cr2O72- + 6 I- + 14 H+ = 2 Cr3+ + 3 I2 + 7 H2O
Z bilansu elektronów wynikają współczynniki: 1 Cr
2O72- oraz 6 I- . Niekiedy spotyka się zapis oddawania 2 elektronów, "ponieważ po stronie produktów jod występuje w postaci dwuatomowych cząsteczek". Jest to błąd, ponieważ celem procedury jest wyznaczenie najpierw współczynników po lewej stronie równania. Gdyby anion jodkowy oddawał dwa elektrony, to produktem jego utlenienia byłby nie jod pierwiastkowy, ale jakiś związek jodu o stopniu utlenienia +1! Zapisanie 2e oddawanych przez anion jodkowy nie pozwoli na ostateczne zbilansowanie równania. Jeśli wyznaczone współczynniki są np. ułamkowe, to dopiero po zakończeniu procedury wyznaczania współczynników stechiometrycznych przy cząsteczkach utleniacza i reduktora można całe równanie pomnożyć przez odpowiednią liczbę (np. 2).Równanie (1) wymaga jeszcze jednego komentarza. Zapis ten sugeruje, że utleniaczem jest atom chromu w anionie dwuchromianowym. Definicja elektrowartościowości zdaje się to potwierdzać: jest to ładunek, jaki miałby dany atom, gdyby zerwane zostały wszystkie wiązania łączące go z innymi atomami cząsteczki. Sugerowałoby to, że atom chromu w anionie dwuchromianowym ma bardziej dodatni ładunek, niż atom chromu w kationie Cr3+. W rzeczywistości może być odwrotnie! Zupełnie poprawnie: nie da się ustalić metodą "na papierze", który atom anionu dwuchromianowego jest utleniaczem. Utleniaczem przyjmującym elektrony jest zespół składający się z dwóch atomów chromu związanych z siedmioma atomami tlenu, posiadający podwójny ładunek ujemny. Dla chemika - praktyka powinno to być zupełnie wystarczające. Szczegółowe wyjaśnienie tego problemu znajdzie Czytelnik w przedostatniej cytowanej pozycji literatury.
Poniższe przykłady są dowodem, że przypisywanie sensu fizycznego stopniom utlenienia nie tylko jest nieporozumieniem, ale jest wręcz błędem metodycznym!
zerowy stopień utlenienia
W niektórych cząsteczkach stopień utlenienia atomu wchodzącego w skład związku chemicznego i tworzącego wiązanie chemiczne z innym atomem tej cząsteczki, równy jest zero.
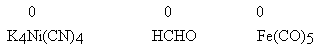
Dodatkowym, choć mniej istotnym, problemem jest kwestia zapisu tej liczby. W zalecanej notacji rzymskiej nie ma w ogóle takiej cyfry; zero genialnie wymyślili znacznie później Arabowie. Równie trudne jest zapisywanie ułamków. Stopnie utlenienia zapisywane są więc cyframi arabskimi. Powoduje to jednak wątpliwości podczas bilansowania: stopnie utlenienia mylą się z fizycznymi ładunkami jonów. W taki sposób pogłębia się tylko zamieszanie pojęciowe! Zalecenia oficjalne zdają się nie dostrzegać tych trudności.
fikcyjność i dowolność
W wielu innych cząsteczkach stopień utlenienia atomu nie ma nic wspólnego ze stanem wiązalności tego atomu:
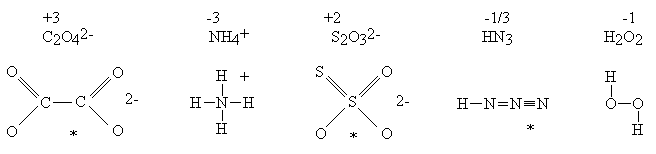
*Czytelnik proszony jest o umowne potraktowanie tych wzorów. Przedstawienie budowy podobnych cząsteczek jednym wzorem, bez wprowadzenia pojęcia mezomerii, jest niemożliwe.
W anionie tiosiarczanowym istnieją dwa różnie związane atomy siarki. Stwierdzenie, że stopień utlenienia siarki wynosi +2 ma taki sam sens jak stwierdzenie, że autor tego opracowania i jego pies mają po trzy nogi (średnio!). Wartością taką można posługiwać się tak długo, jak długo pamięta się, że nie ma ona nic wspólnego z rzeczywistością (autor nie jest mutantem, zaś pies nie jest inwalidą). Wypadałoby zatem, wprowadzając pojęcie stopnia utlenienia, uczynić takie zastrzeżenie i zadbać o to, aby zostało ono zrozumiane przez słuchaczy. Można łatwo sprawdzić, że ani autorzy podręczników, ani wykładowcy takiej uwagi nie czynią (czyżby sami nie zdają sobie z tego sprawy?). Skutkiem tego jest powszechne mylenie stopni utlenienia ze stanem wiązalności atomów. Stopnie utlenienia nazywane są czasem "pożyteczną fikcją". Wydaje się jednak, że (tak jak każda fikcja) przynoszą więcej szkody niż pożytku.
W anionie tiosiarczanowym jeden atom siarki może mieć stopień utlenienia -2, a drugi +6. Potwierdzać to mogłaby skłonność tiosiarczanu do tworzenia w środowisku zasadowym anionów siarczkowych:
S2O32- + OH- = HS- + SO42-
Reakcja ta podawana jest jako przykład dysproporcjonowania. Równie dobrze może być ona potraktowana jako reakcja podstawienia, a nie jako reakcja redukcji-utlenienia. Można wreszcie przyjąć stopnie utlenienia: 0 i +4. I nie jest to wcale sprzeczne z podaną wcześniej regułą ustalania stopni utlenienia.
Obliczanie stopni utlenienia atomów węgla w związkach organicznych prowadzi do karkołomnych rezultatów. Stopień utlenienia atomów węgla w cząsteczkach organicznych zmienia się w granicach: od -4 w CH
4 do +4 w CO2. Katenacja traktowana jest jako proces utleniania-redukcji. Niekiedy dydaktycy proponują specjalne procedury dla tej klasy związków, traktując np. wiązania pomiędzy atomami węgla jako nie istniejące. Jest to procedura sztuczna, nie mająca żadnego rozsądnego uzasadnienia, niepotrzebnie obciążająca pamięć, a w gruncie rzeczy zupełnie zbędna.Ustalenie stopni utlenienia jest niekiedy niemożliwe bez uprzedniej znajomości faktów chemicznych. Przykład: utlenianie nadsiarczanem można opisywać dwoma sposobami
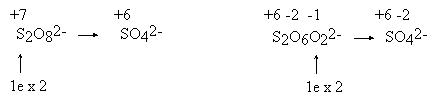
W drugim opisie traktuje się stan wiązalności (i stan utlenienia) atomów siarki u obu reagentów jako identyczny (+6). W takim razie w anionie nadsiarczanowym istnieją dwa rodzaje atomów tlenu: jedne "zwykłe", takie same jak w anionie SO
42- , oraz inne, o stopniu utlenienia wyższym niż -2 (a więc -1). Na pierwszy rzut oka drugi opis robi wrażenie co najmniej dziwaczne, jest on jednak zgodny z naszą wiedzą chemiczną (fakt ten ma zresztą odbicie w poprawnej nazwie: dwunadtlenosiarczan). Toczenie sporu podczas wyznaczania współczynników w równaniu o to, który z tych zapisów jest prawidłowy jest nieporozumieniem: oba pozwalają na uzyskanie poprawnych współczynników. Naprawdę nie ma powodu, aby tolerować sensowność stopnia utlenienia siarki +2 w tiosiarczanie, a dyskryminować operowanie stopniem utlenienia +7 w nadsiarczanie! Obie te wielkości są bowiem równie fikcyjne...Podobne problemy może sprawiać ustalenie stopni utlenienia w dwóch podobnych na pozór związkach: MnO
2 i BaO2. Chemik wie, że jeden z tych związków jest zwykłym tlenkiem, a drugi nadtlenkiem. Natomiast laik, pozbawiony tej wiedzy, jest wobec tego problemu bezradny. Jeśli jednak nie przejmuje się on zbytnio problemami chemicznymi, otrzyma poprawne równanie używając obliczonych w dowolny sposób stopni utlenienia.Interesująca jest próba zapisania równania reakcji tiosiarczanu z nadsiarczanem, w wyniku której powstaje obok siebie czterotionian i siarczan. Okazuje się, że możliwe są dwa rozwiązania:
Otrzymuje się w każdym przypadku równanie o zupełnie innej stechiometrii!
Z powodów wyjaśnianych uprzednio, przyjęto stopień utlenienia siarki w nadsiarczanie, jako równy +7.
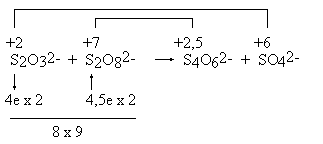
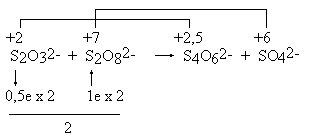
2 S2O32- + S2O82- = S4O62- + 2 SO42-
9 S2O32- + 8 S2O82- + 5 H2O = 4 S4O62- + 18 SO42- + 10 H+
W przypadku związków siarki często istnieje możliwość podobnie skomplikowanego biegu wielu reakcji równoległych. Jest to przyczyna, dla której w tego typu układach (zawierających związki siarki) występują czasami zjawiska oscylacyjne.
Wracając do wcześniejszego przykładu, równie dobrze można przyjąć, że stopień utlenienia atomu węgla w cząsteczce formaldehydu HCHO wynosi +4, zaś stopień utlenienia obu atomów wodoru równy jest -1 (tak, jak w anionie wodorkowym!). Są fakty doświadczalne, które zdają się to potwierdzać. W reakcji formaldehydu z nadtlenkiem wodoru wydziela się bowiem znaczna ilość wodoru. Skoro w wyniku utleniania powstaje wodór gazowy (stopień utlenienia 0), to w cząsteczce substratu atomy wodoru mają niższy stopień utlenienia, a więc -1. Reakcja ta będzie opisana dokładniej w końcowej części opracowania. Powoływanie się na dane doświadczalne przy określaniu stopni utlenienia, spowodowane brakiem precyzyjnych reguł, może być jednak dowodem braku konsekwencji.
Kolejnym przykładem może być ustalenie stopni utlenienia atomów w anionie rodankowym. Możliwe są co najmniej dwa opisy:

Nieco dalej będziemy starali się nieco przekornie wykazać, że stopień utlenienia atomu siarki w tym anionie wynosi 0. W żadnym razie nie można wyciągnąć jednak z tego wniosku, że atom siarki w anionie rodankowym nie jest w ogóle połączony wiązaniem chemicznym z resztą anionu! Oto przykład, jak silnie zakorzenione jest mylenie stopni utlenienia ze stanem wiązalności atomów.
W celu wyznaczenia współczynników w równaniach reakcji chemicznych można z powodzeniem stosować
kompletnie fikcyjne wartości stopni utlenienia. Niech świadczy o tym poniższy przykład. Zanim jednak Czytelnik przeczyta dalszy fragment tekstu, proszę o próbę samodzielnego wyznaczenia współczynników w równaniu:P2I4 + P4 + H2O -> PH4I + H3PO4
Zastosowanie "racjonalnych chemicznie" stopni utlenienia do atomów fosforu (odpowiednio: +2, 0, -3, +5) prowadzi do nieoczekiwanych kłopotów wynikających z faktu, że atomy fosforu są zarówno utleniaczem, jak i reduktorem, a na dodatek po każdej stronie równania występują dwa rodzaje substancji zawierających fosfor. Kłopotów tych można uniknąć przyjmując fikcyjnie (!), że w reakcji uczestniczą tylko dwa rodzaje związków fosforu: fosfor pierwiastkow
y (stopień utlenienia 0) oraz związki fosforu na stopniu utlenienia +5 (sic!). Stąd wynikają stopnie utlenienia atomów jodu: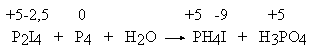
Po dokonaniu bilansu liczby elektronów, Czytelnik w prosty sposób doprowadzi to równanie do postaci:
10 P2I4 + 13 P4 + 128 H2O = 40 PH4I + 32 H3PO4
Posługiwanie się taką procedurą prowadzi co prawda do poprawnego wyniku, ale każdy chemik powinien być zbulwersowany stopniem utlenienia jodu -9 w jodku fosfoniowym! Taki sposób nie pozwala na ustalenie, jakie atomy są partnerami procesu redoks. Zależy to bowiem od sposobu obliczania stopni utlenienia. Nie ma to jednak większego znaczenia, gdyż rozstrzygnięcie tego problemu na papierze i tak nie jest możliwe. W dalszej części opisane będą jeszcze inne, prostsze metody wyznaczania
współczynników w tym skomplikowanym równaniu.Rozwiązanie cytowanego w dalszej części opisu tzw. "równania Stouta" (utlenianie kompleksu chromu, cyjanków i mocznika) jest dosyć kłopotliwe. Wzór całej cząsteczki można jednak zapisać w postaci sumarycznej: Cr
7N66H96C42O24. Następnie można fikcyjnie (!) przyjąć, że w wyniku reakcji zmienia się jedynie stopień utlenienia chromu, zaś pozostałe atomy tego kompleksu nie zmieniają stopni utlenienia (!). Wynikiem takich założeń jest mocno egzotyczny stopień utlenienia chromu: -546/7. Przeprowadzenie bilansu elektronowego daje w wyniku współczynniki identyczne jak te, które opisane są dalej przy metodzie algebraicznej.Należy wreszcie powiedzieć w tym miejscu, że wiele równań daje się zapisać w dwóch równoważnych for
mach:IO3- + 5 I- + 6 H+
= 3 I2 + 3 H2O
IO3- + 5 I- + 3 H2O = 3
I2 + 6 OH-
Dodatkowy wniosek z obu zapisów jest identyczny: zajściu reakcji towarzyszy wzrost pH. Rozstrzygnięcie, która z nich jest poprawna, jest możliwe jedynie na drodze doświadczalnej. Z punktu widzenia formalnego oraz stechiometrii chemicznej, oba zapisy są równocenne. Należy więc zaapelować do egzaminatorów o wyrozumiałość w ocenie takich zapisów przez nie mających doświadczenia praktycznego Studentów.
W praktyce dydaktycznej spotykamy się czasem z zapisem, który dla początkującego słuchacza jest zupełnie niejasny, np. zapis równania utleniania nadmanganianem w środowisku kwaśnym:
Mn (VII) + 5e -> Mn (II)
Reasumując: stosowanie stopni utlenienia pozwala na wyznaczanie współczynników w równaniach reakcji tylko niektórych rodzajów (utleniania-redukcji), opiera się na fikcyjnych wielkościach, które powodują pojęciowe zamieszanie, zaś w niektórych przypadkach ustalenie i zastosowanie stopni utlenienia jest bardzo kłopotliwe.
"PING-PONG" - METODA KOLEJNYCH KONTROLI
Istnieje procedura (w gruncie rzeczy jest to uproszczona metoda algebraiczna) abstrahująca od takich przesłanek chemicznych jak pojęcia reduktora - utleniacza, redukcji - utlenienia oraz stopni utlenienia. Jest to więc metoda bardziej uniwersalna od opisanej poprzednio. Niezbędne jest jednak wstępne prawidłowe ustalenie rodzaju substancji będących substratami i produktami. Procedura polega na wyszukaniu atomów takiego rodzaju pierwiastka, który występuje po lewej i
po prawej stronie równania tylko raz. Wynikają stąd w oczywisty sposób odpowiednie współczynniki stechiometryczne. Przykładem niech będzie opisane przedtem kłopotliwe równanie reakcji jodku fosforu. Wyróżnionymi atomami są atomy tlenu. Kolejne etapy postępowania oznaczone są na schemacie: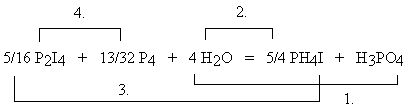
Współczynnik 5/4 PH
4I wynika z odjęcia od 8 atomów wodoru (4 H2O) po lewej stronie równania, 3 atomów wodoru po prawej stronie równania (H3PO4). Z bilansu liczby atomów jodu wynika współczynnik 5/16 P2I4, natomiast z bilansu liczby atomów fosforu po obu stronach równania wynika współczynnik 13/32 P4. Po obustronnym pomnożeniu współczynników przez 32, otrzymuje się przytoczone wcześniej rozwiązanie. Równanie, które sprawiało tyle kłopotów w procedurze chemicznej, daje się rozwiązać w tak prymitywny sposób! Metoda ta nazwana może być metodą kontroli (ang.: Inspection Method), a z powodu kolejnego przechodzenia z jednej strony równania na drugą "metodą ping-pong". W przypadku równań reakcji z udziałem jonów, ostatnim etapem jest kontrola zgodności ładunków jonów. Sposób ten jednak zawodzi w niektórych przypadkach. Proponowana jest zatem jego rozwinięta wersja.PODWÓJNY "PING-PONG"
Cząsteczki zawierające atomy takich pierwiastków, które występują po każdej stronie równania tylko raz, porównywane są w pierwszej kolejności. Wyrażenia zawierające atomy tego samego pierwiastka, które są ze sobą porównywane, tworzą "połączony zestaw". Zwykle w równaniu powstają dwa takie zestawy. Jeśli jakaś substancja należy jednocześnie do
obu zestawów, zapisuje się ją dwukrotnie.Pb(N3)2 + Cr(MnO4)2 -> Pb3O4 + NO + Cr2O3 + MnO2
Bilans atomów ołowiu (Pb
3O4) wymaga wstawienia 3 Pb(N3)2 po lewej stronie równania, a w konsekwencji - wstawienia 18 NO po prawej stronie. Te trzy wyrażenia tworzą jeden zestaw. Pozostają niezbilansowane atomy tlenu. Po prawej stronie jest ich nadmiar: 22 atomy.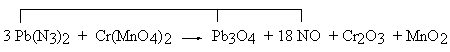
Drugi zestaw tworzą: 2 Cr(MnO
4)2, Cr2O3 oraz 4 MnO2. Również w tym zestawie atomy tlenu nie są zbilansowane; po prawej stronie brak jest 5 atomów tlenu. Zaznaczono to na schemacie.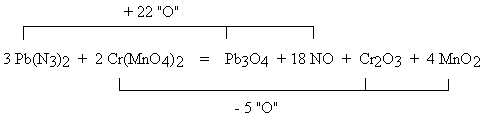
Aby oba zestawy zbilansować, pierwszy z nich trzeba pomnożyć przez 5, a drugi pomnożyć przez 22.
15 Pb(N3)2 + 44 Cr(MnO4)2 = 5 Pb3O4 + 90 NO + 22 Cr2O3 + 88 MnO2
Opisana procedura jest niesłusznie lekceważona. Proszę Czytelnika o sprawdzenie, że tzw. "równanie Stouta", którego kłopotliwa algebraiczna metoda rozwiązania jest opisana nieco dalej, najwygodniej jest zapisywać właśnie w sposób omawiany w tym miejscu.
RÓWNANIA POŁÓWKOWE
Równania połówkowe polegają na rozłożeniu reakcji redoks na dwa* procesy cząstkowe, w
* a właściwie skąd wiadomo, że w sumarycznej złożonej reakcji redoks nie może brać udziału więcej procesów cząstkowych? Takie założenie ogranicza przecież liczbę rozwiązań! Nieco dalej opisane będą interesujące przykłady takich reakcji.
których pojawiają się wolne elektrony. Zbilansowanie polega na takim dobraniu współczynników, aby liczba elektronów oddawanych w jednej reakcji połówkowej była równa liczbie elektronów przyjmowanych w drugiej z reakcji połówkowych.
Z naciskiem należy podkreślić, że zapis równań połówkowych ma pozwalać na ominięcie niejednoznaczności związanych z pojęciem stopnia utlenienia. Nagminnym błędem dydaktycznym jest więc wyznaczanie współczynników w równaniu połówkowym właśnie w oparciu o stopnie utlenienia.
Celem zapisywania równania połówkowego jest bowiem wyznaczenie liczby wymienianych elektronów. Dokonuje się tego w wyniku prostych rachunków bilansu atomów poszczególnych rodzajów po obu stronach równania, ewentualnym uzupełnieniu brakujących typowych elementów (H+, H2O, OH-) i dokonaniu bilansu fizycznych ładunków jonów (a nie: abstrakcyjnych stopni utlenienia!), a na koniec wyznaczenie brakujących po jednej ze stron równania liczby elektronów czyli brakujących ładunków ujemnych. Kolejne etapy są następujące:bilans atomów Cr:
Cr2O72-
-> 2 Cr3+
bilans atomów O:
Cr2O72- -> 2 Cr3+
+ 7 H2O
bilans atomów H:
Cr2O72- + 14 H+ ->
2 Cr3+ + 7 H2O
bilans ładunków jonów: Cr2O72-
+ 14 H+ + 6e -> 2 Cr3+ + 7 H2O
Okazuje się, że do zapisania tego równania nie trzeba było stosować stopni utlenienia, ani też znać właściwości substancji. Właściwości utleniające (a nie: redukujące) dwuchromianu wynikają niejako automatycznie z przeprowadzonych rachunków. Jest to wniosek bulwersując
y, ponieważ jedynymi przesłankami do jego uzyskania był wzór (skład) substratu i produktu. Czyżby więc to, że jakaś substancja jest utleniaczem, wynikało tylko ze stosunków liczbowych określających wzór związków? Jakże tak? A gdzie stopnie utlenienia, Układ Okresowy, pojęcie elektroujemności, równanie Schrödingera i pozostała wiedza chemiczna?! Takie twierdzenie graniczy o krok z kabalistyką... Nieco później posuniemy się w podobnym rozumowaniu jeszcze dalej.Wielu chemików lubi posługiwać się równaniami połówkowymi uważając, że odzwierciedlają one "rzeczywistą naturę" procesów chemicznych - w odróżnieniu od sumarycznych równań reakcji. Niestety, jest to przekonanie błędne. Jeśli w równaniu połówkowym bierze udział więcej cząstek substratów niż dwie (a tak j
est najczęściej), to z pewnością równanie takie jest sumą kilku procesów elementarnych. Należy pamiętać, że w całej chemii nie jest znana ani jedna reakcja, której mechanizm jest więcej niż dwucząsteczkowy (niezależnie od postaci równania ogólnego)! Również opieranie zapisu równania Nernsta na równaniach połówkowych może być zawodne... Doświadczalne zależności polarograficzne mogą być również sprzeczne z równaniami połówkowymi redoks.Na razie Czytelnik proszony jest o algebraiczne udowodnienie w opisany sposób (bez posługiwania się stopniami utlenienia!), że procesy:
Cr2O72- -> CrO42- oraz: AsO2- -> AsO33-
nie są reakcjami połówkowymi utlenienia-redukcji.
reakcja tiosiarczanu z nadsiarczanem prowadząca do czterotionianu i siarczanu:
Dla reagentów: S2O32-, S4O62- , S2O82- i SO42- można zaproponować sześć równań reakcji połówkowych:
2 S2O32-
-> S4O62- + 2eIstnieje nieskończenie wielka liczba możliwości zbilansowania tego zestawu równań, dlatego metoda równań połówkowych jest nieprzydatna w tym przypadku. Najbardziej ogólny zapis równania sumarycznego tej reakcji zaprezentowany będzie przy omawianiu metody algebraicznej.
utlenianie rodanków:
Problemem sygnalizowanym uprzednio było ustalenie stopni utlenienia atomów (szczególnie atomu siarki) w anionie rodankowym. Pewne wskazówki może dać analiza równania reakcji utleniania rodanków:
SCN- -> SO42- + CN-
Zapis równania połówkowego pozwala na wyznaczenie liczby wymienianych elektronów:
SCN- + 4 H2O -> SO42- + CN- + 8 H+ + 6e
Nie sposób nie zauważyć formalnej analogii z zapisem utleniania pierwiastkowej siarki:
S + 4 H2O -> SO42- + 8 H+ + 6e
Czyżby zatem można przyjąć, że stopień utlenienia siarki w rodankach jest taki sam jak w siarce pierwiastkowej - czyli zero? A jeśli tak, to reakcja tworzenia rodanków:
S + CN- -> SCN-
nie jest reakcją utlenienia-redukcji?
A reakcja utleniania cyjanków do cyjanianów?
O + CN- -> OCN-
kłopotliwe pytanie
W tym miejscu trzeba zapytać, co to właściwie są reakcje utlenienia-redukcji. Kryterium zmiany wartości stopnia utlenienia nie jest właściwe z powodu jego niejednoznaczności, a wręcz dowolności ich obliczania. W podręcznikach definiuje się je jako procesy polegające na wymianie elektronów. W przypadku reakcji, które dają się rozdzielić na odpowiednie reakcje połówkowe, jest to jednoznaczne. Problem stwarzają wewnątrzcząsteczkowe reakcje redoks, w których równaniu nie
pojawiają się wolne elektrony. Przykładem niech będzie reakcja termicznego rozkładu azotynu amonu:NH4NO2 -> N2 + 2 H2O
W równaniu tym nie pojawiają się wolne elektrony. Jeśli przyjąć, że stopnie utlenienia atomów azotu w azotynie amonu wynoszą odpowiednio: -3 i +3 - to trzeba uznać, że jest to oczywiście reakcja utlenienia-redukcji. Jednak jeśli przyjąć, że stopnie utlenienia obu atomów azotu wynoszą 0 (NH
4NO2 = N2H4O2), to reakcja ta nie będzie mogła być uważana za reakcję utlenienia-redukcji. Autor nie zamierza w ten sposób sugerować, że azotyn amonu jest tym samym, co "hydrat azotu", jednak nikt nie ma wątpliwości, że w podobnej cząsteczce formaldehydu HCHO = CH2O stopień utlenienia węgla wynosi 0. Być może Czytelnik zna mniej bulwersujący sposób opisu stopni utlenienia w tych cząsteczkach*. Warto przypomnieć, że stopień utlenienia siarki +2 w tiosiarczanie* Podobna sytuacja dotyczy cząsteczki glukozy C
6H12O6 = C6(H2O)6. Na podstawie takiego dziwacznego zapisu nikt nie twierdzi, że glukoza jest mieszaniną równomolowych ilości węgla i wody! A jednak jeszcze w ubiegłym wieku cukry nazywane były powszechnie "wodzianami węgla". Dopiero nie tak dawno rozpowszechniła się nazwa "węglowodany", co prawda błędna gramatycznie, ale nie zawierająca nieprawdziwych chemicznie sugestii. Dawne nazwy przetrwały do dziś w innych językach, jako: "carbohydrates", "Kohlenhydraten" lub "ugliewody".ustalano w oparciu o sumaryczny wzór związku, bez uwzględniania różności obu atomów siarki. Dlaczego więc nie postępować tak samo z azotynem amonu?
Wracając do postawionego pytania: jeśli uznać przedstawione wyżej przesłanki, to autor nie podejmuje się podania definicji reakcji utlenienia-redukcji! Pewnym pocieszeniem niech będzie fakt, że na to pytanie nie potrafił odpowiedzieć jednoznacznie nikt z uczestników Szkoły Problemów Dydaktyki Chemii w 1985 roku... Właściwie wszystkie reakcje chemiczne polegają na zmianie konfiguracji i gęstości elektronowej wokół reagujących atomów. Zatem wszystkie reakcje chemiczne możnaby uznać za re
akcje redoks. W tym miejscu zaprotestują słusznie chemicy-praktycy. Podział na reakcje utlenienia-redukcji i reakcje inne wynika bowiem z bardzo praktycznych różnic doświadczalnych. Wobec trudności zdefiniowania, może warto byłoby powrócić do dawnej prymitywnej definicji: utleniaczem jest substancja, która powoduje zmianę koloru bezbarwnego roztworu jodku potasu z dodatkiem skrobi - na niebieski, zaś reduktorem substancja powodująca odbarwienie zakwaszonego roztworu nadmanganianu potasu? Taka "praktyczna" forma definiowania nie jest w chemii precedensem; mało kto zdaje sobie sprawę, że w podobny sposób zdefiniowano oficjalnie wielkość pH.Ktoś mógłby zwrócić uwagę, że ostatnie równanie można rozdzielić na dwa równania połówkowe jonów:
NH4+ -> 1/2 N2
+ 4 H+ + 4e
NO2- + 4 H+ + 4e -> 1/2 N2
+ 2 H2O
Bez trudu jednak można podać przykłady substancji, w przypadku których taki zabieg jest niemożliwy:
2 C3H5O9N3 -> 6 CO2 + 5 H2O + 3 N2 + 1/2 O2
Reakcja zachodząca podczas wybuchu trójazotanu gliceryny (nitrogliceryny), jest z powodów zwyczajowych i historycznych zaliczana do wewnątrz cząsteczkowych reakcji utleniania-redukcji. Czytelnik może jednak mieć kłopot z racjonalnym uzasadnieniem takiej tezy...
Jak zatem, po tylu krytycznych uwagach, powinni chemicy zapisywać równania reakcji? Jeśli fikcja stopni utlenienia prowadzi do poprawnych rezultatów, to czy w ogóle ma sens posługiwanie się nią? Czy nie lepiej korzystać z bardziej pierwotnych przesłanek? Ponieważ stopnie utlenienia oblicza się (niestety, czasem w dowolny sposób) na podstawie składu (wzoru) cząsteczek, zatem taką pierwotną wielkością powinien być skład (wzór) cząsteczki. Na tym opiera się procedura algebraiczna, najbardziej ogólna metoda, abstrahująca od jakichkolwiek przesłanek chemicznych (poza wzorami substancji), dająca jednak zaskakujące wnioski natury chemicznej, a pozwalająca dodatkowo na wykrywanie popełnianych błędów.
PROCEDURA ALGEBRAICZNA
Niżej zostaną przedstawione zasady tej procedury, a następnie przykłady rodzajów rozwiązań. Czytelnik proszony jest teraz o tymczasowe usunięcie z pamięci takich przesłanek chemicznych, jak stopnie utlenienia, pojęć utleniacza i utleniania, reduktora i redukcji, bilansu elektronów, reguł dotyczących uwzględniania substancji dodatkowych ( takich jak woda, jony
wodorowe) oraz zapisywania substratów po lewej, a produktów po prawej stronie równania. Już w tym miejscu należy zwrócić uwagę, że jest to więc najbardziej uniwersalny z opisywanych sposobów zapisywania równań chemicznych. W tej procedurze identycznie traktowane są zarówno reakcje będące, jak i nie będące reakcjami redoks, reakcje połówkowe, a wreszcie reakcje związków organicznych. Aby opis uczynić bardziej interesującym, w przykładach celowo popełniane będą błędy oczywiste dla doświadczonego chemika, a sprawiające trudność laikowi. Jeśli procedurę algebraiczną potraktować jako formę dialogu, to wypada stwierdzić, że jest to metoda całkowicie odporna zarówno na niezamierzone błędy, jak i celowe próby oszustwa (!). Fascynujący jest sposób, w jaki uzyskuje się informacje o popełnionych błędach lub zaskakujące wskazówki o czysto chemicznym charakterze. Dialog prowadzony będzie w języku algebry elementarnej.Wzory substratów i produktów zapisuje się po obu stronach równania. Kolejnym reagentom przypisuje się współczynniki:
a, b, c, d itd. Układa się następnie równania bilansowe dla wszystkich rodzajów atomów biorących udział w reakcji oraz dla ładunków jonów reagentów. Po rozwiązaniu tego układu równań, otrzymuje się konkretne wartości współczynników stechiometrycznych. Tak jak zawsze w algebrze, możliwe są trzy grupy rozwiązań: brak rozwiązań, jedno rozwiązanie oraz nieskończenie wielka liczba rozwiązań takiego układu równań.Brak rozwiązań
rozkład kwasu siarkowego na SO
2:a H2SO4 -> b H2O + c SO2
bilans atomów H: 2a = 2b
bilans atomów S: a = c
bilans atomów O: 4a = b + 2c
Rozwiązując układ równań otrzymujemy: a = 0, b = 0, c = 0.
Tłumacząc wynik algebraiczny na język chemiczny oznacza to, że taka reakcja zachodzi wtedy, kiedy nie biorą w niej udziału żadne reagenty! Przyczyna jest oczywista dla każdego chemika: popełniono błąd, ponieważ produktem odwodnienia kwasu siarkowego nie jest SO
2, ale SO3, lub mieszanina SO2 i tlenu! Laik, popełniwszy taki błąd, mógłby jednak długo i bezskutecznie męczyć się przy stosowaniu typowo chemicznej procedury ustalania współczynników.Ponieważ rozwiązywanie układu równań jest tym łatwiejsze, im mniej jest niewiadomych, zatem w typowej procedurze algebraicznej przyjmuje się arbitralnie jeden współczynnik (zazwyczaj przy reagencie o najbardziej skomplikowanej budowie), jako równy np. 1 (równie dobrze: 2 lub 3), a współczynniki przy kolejnych reagentach staramy się wyrażać za pomocą parametrów już wprowadzonych - tam, gdzie jest to zupełnie oczywiste. Wstawienie w poprz
ednim równaniu współczynnika 1 w miejsce parametru "a" trzeba uznać za próbę "oszukania" procedury. Interesujące, czy istotnie w taki sposób można będzie uzyskać wynik inny od poprzedniego rezultatu?1 H2SO4 -> b H2O + c SO2
bilans atomów H: 2 = 2b
bilans atomów S: 1 = c
bilans atomów O: 4 = b + 2c
Ten układ równań jest układem sprzecznym i nie ma rozwiązań.
Wniosek z obu przykładów: taka reakcja jest niemożliwa. Albo nie powstaje SO
2, albo pominięto jeden z produktów. Procedura algebraiczna okazuje się rzeczywiście odporna na tego rodzaju błędy lub manipulacje... Należy pamiętać, że otrzymane rozwiązania muszą spełniać wszystkie równania bilansowe.ze związkami chromu:
Czytelnik z pewnością potrafi podać chemiczną interpretację algebraicznego rozwiązania (a raczej: powodu braku rozwiązań) kolejnego równania:
Cr(OH)4- -> CrO42- + x H2O + 2x H+
Jest to bowiem równanie połówkowe redoks, w którym jednak pominięto omyłkowo jeden z reagentów - elektrony.
W procedurze algebraicznej można omyłkowo dowolnie zamienić stronami substraty i produkty reakcji. Również zapisanie "środowiska" po niewłaściwej stronie nie stanowi żadnego problemu. Obliczone współczynniki w takich przypadkach będą miały wartość ujemną.
Jedno rozwiązanie
Prawie wszystkie przypadki prawidłowo zapisanych równań reakcji chemicznych dają w wyniku jeden zespół konkretnych rozwiązań: dodatnich, ujemnych lub ułamkowych. Niektóre parametry mogą być równe zero.
równanie reakcji azotanów z udziałem anionów glinianowych oraz glinu:
NO3- + a AlO2- + b H2O -> NH3 + a Al + c OH-
bilans atomów O: 3 + 2a + b = c
bilans atomów H: 2b = 3 + c
bilans ładunków:
- 1 - a = - c
bilanse atomów N i Al są tautologiami typu: 1 = 1
Rozwiązanie: a = -8/3, b = 2/3, c = -5/3.
Aniony azotanowe reagują z metalicznym glinem, a nie z anionami glinianowymi! AlO2- jest jednym z produktów reakcji, natomiast jony OH- są substratem, a nie produktem.
3 NO3- + 8 Al + 2 H2O + 5 OH- = 3 NH3 + 8 AlO2-
Zamiast współczynnika c - w celu ograniczenia liczby zmiennych i uproszczenia obliczeń - można wstawić wartość: (1+a), która wynika z bilansu ładunków. Procedura ta dałaby identyczny wynik.
w postaci "kanonicznej":
NO3- - NH3 + a Al - a AlO33- + b H2O + c OH- = 0
Współczynnik przy NH
3 jest liczbowo równy współczynnikowi przy NO3-, ale musi mieć przeciwny znak, gdyż te dwie substancje muszą występować po dwóch różnych stronach równania. Podobnie jak metaliczny glin i anion ortoglinianowy.bilans atomów O: 3 - 3a + b + c = 0
bilans atomów H: -3 + 2b + c = 0
bilans ładunków: -1 + 3a - c = 0
Rozwiązanie: a = 8/3, b = -2, c
= 7.
3 NO3- + 8 Al + 21 OH- = 3 NH3 + 8 AlO33- + 6 H2O
Zachęcam Czytelnika do próby "oszukania" procedury poprzez wstawienie współczynni
ków: - a Al oraz + a AlO33-. Rezultat takiej próby nie jest przypadkowy i powinien dawać do myślenia...kabalistyka?
Ściśle chemiczny charakter wniosków z podanych przykładów skłania do postawienia następujących pytań: Co sprawia, że w układzie reagentów: A, B, C, D możliwa (przynajmniej teoretycznie) jest reakcja np. A + B
-> C + D, a nie jest możliwa (nawet teoretycznie!) reakcja np. A + C -> B + D ? Co właściwie jest przyczyną, że dana reakcja jest lub nie jest procesem redukcji-utleniania (przykład następny)? Przyczyny zdają się tkwić wyłącznie w stosunkach liczbowych określających skład substancji. Taka teza z pewnością wyda się wręcz prowokacyjna dla wielu chemików, którzy skłonni będą zaliczyć ją do swoistej kabalistyki. Podobnych przykładów uważanych kiedyś za kabalistykę w chemii można wymienić znacznie więcej. Począwszy od faktu okresowości właściwości pierwiastków: co ósmy - poprzez empiryczne równania opisujące poszczególne serie widm emisyjnych, co doprowadziło do sformułowania warunków kwantowania i liczb kwantowych - skończywszy zaś na równaniu Hückla opisującym stan aromatyczny. Wszystko to nie oznacza bynajmniej, że z danych algebraicznych można odczytać wszystkie właściwości chemiczne.sumaryczne czy połówkowe?
Również zapisywanie równań połówkowych odbywa się identycznie:
AsO2- + x H2O -> AsO33- + 2x H+ + y e x = 1, y = 0
To równanie nie jest więc równaniem reakcji połówkowej redoks (
y = 0).Natomiast zapisanie równania sumarycznego redoks jako równania połówkowego (z elektronami) prowadzi do nieskończonej liczby rozwiązań. Zostaje ono potraktowane jako suma dwóch równań połówkowych, które nie są zbilansowane. Takich kombinacji niezbilansowanych sum dwóch równań połówkowych jest nieskończenie wiele, w odróżnieniu od jednej tylko sumy równań połówkowych zbilansowanej pod względem liczby wymienianych elektronów.
Cr2O72- + x I- + y H+ -> 2 Cr3+ + x/2 I2 + y/2 H2O + z e
W procedurze algebraicznej zapisywanie równań reakcji związków organicznych nie różni się niczym od
innych reakcji:równanie połówkowe reakcji utleniania winianów:
C4H4O62- + a H+ -> 4 CO2 + b H2O + c e
bilans atomów O: 6 = 8 + b;
b = -2
bilans atomów H: 4 + a = 2b; a = -8
bilans ładunków: - 2 + a = - c;
c
= 10
C4H4O62- + 2 H2O = 4 CO2 + 8 H+ + 10 e
Zbędne jest więc zastanawianie się nad stopniami utlenienia węgla w winianie.
ponownie jodek fosforu:
Czytelnik proszony jest o uzyskanie rozwiązania cytowanej kilkakrotnie kłopotliwej reakcji:
P2I4 + x P4 + y H2O -> 4 PH4I + z H3PO4 x = 13/10 y = 64/5 z = 16/5
równania Stouta i Blakleya:
I wreszcie wytrwałym Czytelnikom proponuję rozwiązanie równania podanego przez Stouta:
[Cr(N2H4CO)6]4[Cr(CN)6]3 + a KMnO4 + b H2SO4 -> c K2Cr2O7 + d MnSO4 + e CO2 + f KNO3 + g K2SO4 + h H2O
Uważny Czytelnik natychmiast spostrzeże, że można zmniejszyć liczbę niewiadomych parametrów:
c=7/2 (jedyne cząsteczki zawierające Cr); d=a (Mn); e=42 (C); f=66 (N), co ułatwi doprowadzenie równania do postaci:10 [Cr(N2H4CO)6]4[Cr(CN)6]3 + 1176 KMnO4 + 1399 H2SO4 = 35 K2Cr2O7 + 1176 MnSO4 + 420 CO2 + 660 KNO3 + 223 K2SO4 + 1879 H2O
A wreszcie zbadanie możliwości rozwiązania różnymi metodami (na koniec - metodą algebraiczną) równania uważanego za wyjątkowo "złośliwe" - tzw. "równania
Blakleya":H2 + a Ca(CN)2 + b NaAlF4 + c FeSO4 + d MgSiO3 + e KI + f H3PO4 + g PbCrO4 + h BrCl + i CF2Cl2 + j SO2 -> k PbBr2 + l CrCl3 + m MgCO3 + n KAl(OH)4 + o Fe(SCN)3 + p PI3 + r Na2SiO3 + s CaF2 + t H2O
Otrzymuje się zestaw 19 równań bilansowych z 19 (!) niewiadomymi. Można co prawda zauważyć, że z oczywistych powodów:
a=s (Ca), b=2r (Na), e=n=b (K,Al), c=o (Fe), f=p (P), g=l (Cr), 2h=k (Br), m=d (Mg), o=2/3a (N) itd. W ten sposób autorowi udało się uprościć równanie do układu 7 równań z 7 niewiadomymi. Czytelnik ma do wyboru: albo żmudnie próbować doprowadzić równanie do rozwiązania podanego niżej, albo zastosować metodę macierzy wzmiankowaną na końcu opisu.88 H2 + 15 Ca(CN)2 + 6 NaAlF4 + 10 FeSO4 + 3 MgSiO3 + 6 KI + 2 H3PO4 + 6 PbCrO4 + 12 BrCl + 3 CF2Cl2 + 20 SO2 = 6 PbBr2 + 6 CrCl3 + 3 MgCO3 + 6 KAl(OH)4 + 10 Fe(SCN)3 + 2 PI3 + 3 Na2SiO3 + 15 CaF2 + 79 H2O
Nieskończenie wiele rozwiązań
Skuteczność metody algebraicznej wypadałoby określić jako przekraczającą 100 %. Nie tylko bowiem daje się w ten sposób zapisać
wszystkie równania reakcji chemicznych, ale metoda pozwala na korygowanie popełnianych błędów. Dodatkowo niekiedy okazuje się, że pod "niewinnie" wyglądającym równaniem kryje się zaskakująco skomplikowany proces, czego nie podejrzewają nawet doświadczeni chemicy... I wszystko to daje się ustalić po prostu na papierze, bez przeprowadzania odpowiednich eksperymentów!Przy próbie zastosowania proponowanej procedury algebraicznej, uzyskuje się czasem układ równań bilansowych mniej liczny niż liczba niewiadomych współczynników. W konsekwencji układ taki ma nieskończenie wiele rozwiązań. Jest to najbardziej interesujący chemicznie przypadek, zazwyczaj będący zaskoczeniem dla chemika. Otrzymanie takiego wyniku jest
wskazówką, że reakcja chemiczna złożona jest z sumy co najmniej dwóch niezależnych, biegnących równolegle procesów. Jest interesujące, że do takiego wniosku można dojść bez przesłanek i intuicji chemicznej. Paradoksalnie, stosując klasyczną procedurę chemiczną, można łatwo przeoczyć grupy rozwiązań mające zupełnie określony sens chemiczny. Metoda algebraiczna jest jedynym sposobem (poza doświadczeniem) wykrycia nieoczekiwanie skomplikowanego przebiegu niektórych pozornie prostych i znanych reakcji chemicznych. Dla większości doświadczonych chemików złożony charakter opisywanych procesów stanie się oczywisty po zakończeniu procedury algebraicznej. A ilu z nich domyśli się tego już przy zapisywaniu początkowego równania?reakcja arseninów z dwuchromianami:
AsO2- + x Cr2O72- + 2y H+ -> AsO33- + 2x CrO42- + y H2O
bilans atomów O: 2 + 7x = 3 + 8x + y
; y = -1-x
bilans ładunków: -1 -2x + 2y = -3 -4x
; 2y = -2-2x
bilanse atomów H, As oraz Cr są tautologiami typu: 1 = 1
Oba równania bilansowe okazują się identyczne. Jest to więc układ jednego równania z dwoma niewiadomymi. Można to równanie uporządkować przez wprowadzenie jednego tylko parametru:
AsO2- + x Cr2O72- + (1+x) H2O = AsO33- + 2x CrO42- + 2(1+x) H+
Równanie to jest spełnione dla każdej wartośc
i x. Mniej uważny Czytelnik, który- zafascynowany algebrą - zbyt dosłownie potraktował polecenie zapomnienia o faktach chemicznych, być może dotąd nie spostrzegł, że cały proces w gruncie rzeczy nie ma sensu. Jest bowiem sumą dwóch niezależnych reakcji (związanych jedynie wspólnym udziałem wody i jonów wodorowych), z których żadna nie jest reakcją utlenienia-redukcji! Nawet jednak laik uzyskuje w tym momencie wskazówkę o złożonym charakterze procesu. Podstawiając: x = 0, a następnie: x -> nieskończoność, można bez trudu zidentyfikować oba procesy składowe. Były one zresztą sygnalizowane już w tym opracowaniu. Czyżby Czytelnik dał się nabrać na taki żart?reakcja siarkowodoru, nadmanganianu potasu, kwasu siarkowego i innych (?) substancji:
Uzupełnić (stosując różne metody), współczynniki w równaniu reakcji:
H2S + KMnO4 + H2SO4 -> S + K2SO4 + MnSO4 + H2O
Pomocna może być analiza następujących równań:
H2S + MnO4- + H+ -> S + Mn2+ + H2O
H2S + MnO4- + H+ ->
SO42- + Mn2+ + H2O
H2S + MnO4- + H+ ->
S + SO42- + Mn2+ + H2O
H2S + y KMnO4 + z H2SO4 -> x S + y/2 K2SO4 + y
MnSO4 + (z+1) H2O
Otrzymuje się układ dwóch równań bilansowych z trzema niewiadomymi.
y = (8-6x)/5 ; z = (7-4x)/5
Czytelnik zechce przeprowadzić analizę pełnego rozwiązania algebraicznego:
5 H2S + (8-6x) KMnO4 + (7-4x) H2SO4 = 5x S + (4-3x) K2SO4 + (8-6x) MnSO4 + (12-4x) H2O
- dla różnych wartości parametru
x, np.: x = 0, x = 1, x = 4/3. Wynik porównać z rezultatami uzyskanymi przy zastosowaniu typowej procedury chemicznej. Przyczyną komplikacji jest fakt, że H2SO4 zapisany jako substrat - "środowisko", może być również produktem utleniania siarkowodoru lub wreszcie substratem - utleniaczem.Wydaje się, że wnioski z takiego rozumowania mogą być zupełnie przeciwne do wniosków sugerowanych w ostatniej z cytowanych pozycji literaturowych. Próba posłużenia się "intuicją chemiczną" w celu ograniczenia liczby rozwiązań może bowiem doprowadzić do pominięcia pewnych rozwiązań, które mają zupełnie konkretn
y - choć czasem zaskakujący - sens chemiczny. Czasami jednak posłużenie się intuicją może być sensowne.utlenianie alkenu:
Czytelnik proszony jest o sprawdzenie, że w równaniu reakcji utleniania 1-metylobutenu-2:
C5H10 + a KMnO4 -> b CH3COOK + c (CH3)2CO + a MnO2 + (a-b) KOH + d H2O
otrzymuje się układ trzech równań bilansowych z czterema niewiadomymi - z wszystkimi konsekwencjami z tego wynikającymi. Dopiero zapisanie wzoru substratu w postaci strukturalnej:
CH3CH=C(CH3)2 + a KMnO4 -> b CH3COOK + c (CH3)2CO + a MnO2 + (a-b) KOH + d H2O
podsuwa sugestię, że z logicznego punktu widzenia współczynniki
b i c muszą być równe 1. Wtedy równanie ma jedno rozwiązanie: a = 2; d = 0reakcja tiosiarczanu z nadsiarczanem:
Nieco wcześniej sygnalizowano już problemy związane ze skomplikowanym przebiegiem tej reakcji. W procedurze algebraicznej wniosek taki można wyciągnąć nie odwołując się do intuicji i wiedzy chemicznej.
S2O32- + x S2O82- + y H2O
-> z S4O62- + w SO42- + 2y H+Uzyskuje się układ trzech równań bilansowych z czterema niewiadomymi: y = (10x-5)/7,
w = (18x-2)/7, z = (4-x)/7 .7 S2O32- + 7x S2O82- + (10x-5) H2O = (4-x) S4O62- + (18x-2) SO42- + (20x-10) H+
Można sprawdzić, że:
dla x = 4: S2O32- + 4 S2O82- + 5 H2O = 10 SO42- + 10 H+
Czytelnik zechce zinterpretować rozwiązania dla wartości parametru x = 0 oraz x -> nieskończoność .
elektroliza nadtlenku wodoru:
Podczas tego niezwykłego procesu powstaje gazowy tlen na anodzie i katodzie (sic!), oraz niewielkie, zmienne ilości wodoru na katodzie.
a H2O2 -> x O2 + y H2 + b H2O
bilans atomów H: 2a = 2y + 2b
bilans atomów O: 2a = 2x + b
Jest to więc układ dwóch równań z czterema niewiadomymi. Można jedynie wprowadzić podstawienie:
a = 2x - y oraz: b = 2x - 2y.(2x-y) H2O2 = x O2 + y H2 + (2x-2y) H2O
Istnieje pokusa, aby zmniejszyć liczbę niewiadomych podstawiając np. w miejsce parametru
b wartość: a-y wynikającą z bilansu atomów wodoru. Zabieg taki nic jednak nie daje, gdyż jedno z równań bilansowych staje się tautologią i w dalszym ciągu liczba niewiadomych pozostaje większa o dwa od liczby równań bilansowych. Wspomniano już przedtem, że procedura algebraiczna jest procedurą inteligentną i jest ona odporna na próby oszustwa...Celowość zapisywania tak ogólnych i mało czytelnych równań może wydawać się wątpliwa. Opisuje jednak ono wszystkie procesy zachodzące w układzie złożonym z H
2O2, H2O, O2 i H2.dla y = 2x czyli dla reakcji w nieobecności H2O2: H2O = H2 + 1/2 O2 - jest to elektroliza wody.
dla y = 0 lub x -> nieskończoność : 2 H2O2 = 2 H2O + O2 - jest to elektroliza zakwaszonego roztworu H2O2 (przy napięciu tak niskim, że można wykluczyć redukcję wody, lub w takich warunkach, w których dominuje uboczna reakcja rozkładu H2O2 w środowisku alkalicznym).
dla x = 0 lub y -> nieskończoność : 2 H2O = H2O2 + H2 - jest to reakcja dysproporcjonowania wody.
Podobne procesy zachodzą podczas produkcji nadtlenku wodoru na skalę przemysłową. Przy elektrolizie dość stężonego roztworu kwasu siarkowego na anodzie powstaje kwas nadtlenodwusiarkowy H
2S2O8, który przenosi się do osobnego naczynia i ogrzewa. Powstaje nadtlenek wodoru, który oddestylowuje do chłodnicy oraz kwas siarkowy, który zawraca się do elektrolizera. Na katodzie wydziela się wodór. Sumaryczny wynik procesu opisuje ostatnie równanie.dla x = - y: H2 + O2 = H2O2 - taka reakcja zachodzi w niewielkim stopniu podczas spalania wodoru. Jeśli płomień wodoru skierować na powierzchnię kostki lodu, to w skroplinach można wykryć obecność niewielkich ilości nadtlenku wodoru.
W tym miejscu należy powiedzieć o przyczynie uzyskiwania niekiedy nieskończonej liczby rozwiązań algebraicznych. Reakcję elektrolizy nadtlenku wodoru można próbować zapisać w postaci sumy równań połówkowych. Każdy chemik natychmiast zaproponuje następującą sumę:
(A) H2O2 = O2 + 2 H+ + 2e
(K) 2 H+ + 2e = H2
Natomiast zapewne niewielu chemików zauważy, że w tej kombinacji reagentów jest jeszcze jedna możliwość - jest to jeszcze jedna reakcja redukcji:
(K) H2O2 + 2 H+ + 2e = 2 H2O
Sumować należy więc nie dwa, a
trzy równania połówkowe! A możliwości zbilansowania jednego równania połówkowego utlenienia wraz z dwoma równaniami połówkowymi redukcji, jest nieskończenie wiele. Zupełnie poprawnie powinno się jeszcze uwzględnić katodową redukcję wody i anodowe jej utlenianie, i jeszcze... W procedurze algebraicznej nie ma jednak potrzeby wykazania się taką bystrością. Wszystkie te możliwości zostaną uwzględnione niejako automatycznie, a osoba rozwiązująca zadanie zostanie o tym poinformowana w postaci nieskończonej liczby rozwiązań! Procedura algebraiczna jest więc nie tylko inteligentna, ale i przyjazna dla chemika...Z analizy postaci algebraicznej rozwiązań omawianych w tym miejscu wynika, że reagowanie ze sobą substratów - a również powstawanie produktów - może przebiegać w zmiennej, a w gruncie rzeczy dowolnej stechiometrii. I tak jest w rzeczywistości. Jest zaskakujące, że do takiego wniosku można dojść na podstawie tylko rachunków na papierze, bez wykonywania jakichkolwiek doświadczeń! Czasami nazywane są one "reakcjami niestechiometrycznymi". Zupełnie poprawnie chodzi t
u o biegnące równocześnie reakcje o zmiennym udziale. Oryginalną cechą tych wszystkich przykładów jest to, że w ramach pewnego zestawu reagentów (substratów-produktów?), istnieje możliwość zachodzenia więcej niż jednej reakcji chemicznej. Rutyna chemiczna powoduje zwykle przeoczenie takiej możliwości (np. przez arbitralne ograniczenie liczby partnerów redoks - do dwóch).reakcja nadmanganianu i nadtlenku wodoru:
Aby móc łatwiej porównać wynik z typowym zapisem podręcznikowym, przyjęto arbitralnie współczyn
nik 2 MnO4-.2 MnO4- + x H2O2 + y H+ -> 2 Mn2+ + w H2O + z O2
bilans atomów O: 8 + 2x = w + 2z
bilans atomów H: 2x + y = 2w
bilans ładunków: -2 + y
= 4
bilans atomów Mn: tautologia typu 1 = 1
Rozwiązanie: y = 6, w = x+3,
z = x/2+2,5
2 MnO4- + x H2O2 + 6 H+ -> 2 Mn2+ + (x+3) H2O + (x/2+2,5) O2
Można sprawdzić, że równanie to jest spełnione i ma ono sens algebraiczny dla każdej wartości "
x", np:x = 0
2 MnO4- + 6 H+ = 2 Mn2+ + 3 H2O +
2,5 O2
x = 1
2 MnO4- + H2O2 + 6 H+ = 2 Mn2+
+ 4 H2O + 3 O2
x = 2
2 MnO4- + 2 H2O2 + 6 H+ = 2 Mn2+
+ 5 H2O + 3,5 O2
x = 5
2 MnO4- + 5 H2O2 + 6 H+ = 2 Mn2+
+ 8 H2O + 5 O2
x -> nieskończoność H2O2
= H2O + 1/2 O2
Czytelnik może spróbować również zinterpretować wyniki otrzymane dla ułamkowych i ujemnych wartości parametru "
x". Procedura taka nie jest jedynie algebraiczną ciekawostką, gdyż niektóre z rozwiązań mają również bardzo konkretny sens chemiczny. Dla x = 0 jest to reakcja rozkładu KMnO4 na tlen, która może zachodzić w bardzo stężonym, silnie zakwaszonym roztworze. Dla x = 5 jest to "klasyczna" reakcja zachodząca podczas miareczkowania nadtlenku wodoru nadmanganianem. Dla x -> nieskończoność otrzymuje się reakcję rozkładu nadtlenku wodoru.Reakcja MnO4- + H2O2 jest właśnie przykładem tzw. "niestechiometrycznej" reakcji chemicznej. W rzeczywistości stanowi ona sumę co najmniej dwóch niezależnych reakcji zachodzących jednocześnie. Są to przede wszystkim: utlenianie H2O2 nadmanganianem (x = 5), oraz katalityczny rozkład H2O2 (x -> nieskończoność ): 2 H2O2 -> 2 H2O + O2.
Ta ostatnia reakcja zachodzi w miejscach słabiej zakwaszonych, w których czasowo powstają pośrednie produkty redukcji nadmanganianu, będące katalizatorami rozkładu nadtlenku wodoru. Powszechnie (choć zasadniczo bezzasadnie) przyjmuje się, że obie te substancje reagują w stosunku 2 mole MnO
4- + 5 moli H2O2. Dzieje się tak jedynie przy silnie zakwaszonym roztworze i powolnym wkraplaniu z jednoczesnym mieszaniem roztworu (x = 5). Ilość tlenu powstająca w reakcji H2O2 z nadmiarem nadmanganianu przy braku mieszania jest zawsze mniejsza od ilości wynikającej z takiej stechiometrii i różnica ta zależy dodatkowo od: stopnia zakwaszenia, kolejności dozowania i sposobu mieszania. Przy wkraplaniu nadmanganianu do nadtlenku wodoru, otrzymuje się mniej tlenu niż przy odwróceniu kolejności! Stwierdzenie takie jest szokujące dla chemika, natomiast laik stosujący procedurę algebraiczną przyjmie to bez zdziwienia. Doświadczalne stwierdzenie tych różnic jest dość kłopotliwe, chociaż ustalenie warunków, w których reakcja ta zachodzi praktycznie według stechiometrii "2+5", było przedmiotem badań.reakcja formaldehydu z nadtlenkiem wodoru:
Bardzo interesujący jest przebieg reakcji stosowanej do miareczkowego oznaczania form
aldehydu w roztworze. Po zaalkalizowaniu próbki znanym nadmiarem NaOH, dodaje się nadmiar H2O2. Formaldehyd przekształca się w kwaśny produkt (HCOOH), a pozostały NaOH odmiareczkowuje się mianowanym roztworem HCl. Zupełną niespodzianką jest jednak rzeczywisty przebieg tego procesu: podczas burzliwej reakcji wydzielają się bowiem znaczne ilości gazowego wodoru! Ciekawe, czy znajdzie się jakiś Czytelnik, który potrafi w tym momencie zapisać metodycznie poprawnie równanie tej reakcji oraz odpowiedzieć, skąd pochodzi gazowy wodór. Klasyczny sposób wyznaczenia współczynników w tym równaniu zupełnie zawodzi.CH2O + x H2O2 + y OH- -> HCOO- + w H2 + z H2O
bilans atomów C: 1 = 1 (tautologia)
bilans atomów O: 1 + 2x + y = 2 + z
bilans atomów H: 2 + 2x + y = 1 + 2w + 2z
bilans ładunków: -y =
-1,
skąd: y = 1, w = 1-x, z = 2x.
CH2O + x H2O2 + OH- = HCOO- + (1-x) H2 + 2x H2O
Na razie trudno jest wytłumaczyć, skąd pochodzi wydzielający się wodór. Okazuje się jednak, że przebieg reakcji jest złożony, a cały proces jest przykładem reakcji "niestechiometrycznej". Jeżeli oprócz reakcji będącej źródłem wodoru, zachodzi równolegle inna reakcja pomiędzy H
2O2 i CH2O, w wyniku której wodór nie powstaje, to ostatecznie ilość gazowego produktu zależy od wzajemnej proporcji udziałów obu tych procesów. Matematyczna analiza ostatniego równania dostarcza potwierdzenia.Dla x = 0 CH2O + OH- -> H-COO- + H2
Otrzymuje się równanie reakcji będącej głównym źródłem wodoru. Proces ten należy określić jako dysproporcjonowanie formaldehydu. W rzeczywistości dysproporcjonuje nie sam formaldehyd, lecz produkt jego przyłączenia do nadtlenku wodoru - nadtlenek dwuhydroksymetylenu:
2 CH2O + H2O2
-> HO-CH2-O-O-CH2-OH
HO-CH2-O-O-CH2-OH + 2 OH- ->
2 HCOO- + H2 + 2 H2O
Nadtlenek z tej reakcji został wyodrębniony i zidentyfikowany.
Dla x = 1 CH2O + H2O2 + OH- -> HCOO- + 2 H2O
Uzyskuje się równanie reakcji której udział poprzednio zanegowano, lecz która może powoli zachodzić w niezbyt silnie zasadowym środowisku. Im większy jest jej udział, tym mniej substratów reaguje według schematu "dysproporcjonowania" i tym mniej powstaje wodoru.
Dla x = 1/2 2 CH2O + H2O2 + 2 OH- -> 2 HCOO- + H2 + 2 H2O
Otrzymuje się równanie obrazujące "przeciętny" przebieg procesu. To równanie można znaleźć w literaturze. Jest ono sumą równań poprzednich reakcji (
x = 0 oraz x = 1).Dla x -> nieskończoność x H2O2 + x H2 -> 2x H2O
Jest to wtórny proces absorpcji wodoru wydzielonego w procesie dysproporcjonowania przez nadtlenek wodoru. Im większy jest udział tej reakcji, tym mniej wodoru się wydziela.
krok dalej: rachunek macierzowy
Rozwiązywanie układów równań z więcej niż trzema niewiadomymi jest ogromnie uciążliwe. Przykładem może być cytowane wcześniej równanie Blakleya. Zastosowanie rachunku macierzowego bardzo ułatwia to zadanie. Co więcej, rachunek macierzowy pozwala na zbudowanie odpowiednich programów komputerowych, zastosowanie rachunku macierzowego, rozszerza prócz tego jakościowo zak
res stosowalności metody algebraicznej.Na stronach Chemfana w dziale Oprogramowanie znajduje się program ChemBalance służący m.in. do uzupełniania współczynników równań reakcji chemicznych (przypis AK).
Podsumowanie
Powyżej opisane rozważania dotyczą jedynie formalnego zapisu równań reakcji chemicznych. Nie rozważano więc w ogóle problemu termodynamicznej możliwości ich zachodzenia.
Chemicy przy zapisywaniu typowych równań utleniania-redukcji będą w dalszym ciągu stosować bilanse elektronowe w oparciu o stopnie utlenienia. Jest to procedura, która jest skuteczna w większości przypadków. Chemikom trudno wyobrazić sobie chemię bez stopni utlenienia. Podświadomie uważają stopnie utlenienia za klucz do zrozumieniu chemii i trudno będzie im zaakceptować fakt, że można się bez stopni utlenienia doskonale obejść. Byłoby dobrze, aby chemi
cy zdawali sobie sprawę z nieścisłości związanych z tym pojęciem oraz pojęciowymi błędami z nim związanymi i uświadamiali te problemy swoim Słuchaczom...Równania połówkowe powinny być rozwiązywane bez wprowadzania stopni utlenienia. Nie powinny być prócz
tego mylone z równaniami elementarnymi mechanizmów reakcji.Warto pamiętać, że istnieją skuteczne metody mnemotechniczne uzupełniania równań ("ping-pong"). To, że nie mają one nic wspólnego z przesłankami chemicznymi jest ich zaletą, a nie wadą.
Chemicy nie będą chętnie posługiwać się procedurą algebraiczną, która jest po prostu dosyć żmudna. Prócz tego nie do przyjęcia emocjonalnego dla chemików jest fakt, że właśnie taka procedura ma największy zakres stosowalności, a prócz tego dostarcza informacji będących czasem zaskoczeniem dla dydaktyków z długoletnim stażem. Warto jednak tę procedurę zastosować wszędzie tam, gdzie zawodzą inne sposoby...
Na rozwiązanie czeka ciągle problem precyzyjnego zdefiniowania reakcji utlenienia-redukcji.
LITERATURA
J.Chem.Educ. 22, 266, 461 (1945). 72, 716, 1125
(1995).
J.Chem.Educ. 36, 215 (1959). 74, 1359 (1997). Kurier Chemiczny.
(1991), Nr 1, str. 6., (1991), Nr 2, str. 6.
[Przegląd metod]
J.Chem.Educ. 38, 327 (1961). 65, 45 (1988). 74, 1270 (1997). 76,
362 (1999). [Krytycznie o stopniach utlenienia]
J.Chem.Educ. 69, 276 (1992). [Reakcja ClO3- + Cl-
-> ClO2 + Cl2]
J.Chem.Educ. 23, 550 (1946). 36, 77 (1959). 74, 69 (1987). 76,
362 (1999). [Organiczne reakcje redoks]
J.Chem.Educ. 38, 329 (1961). 74, 1365, 1365 (1997). [Metoda
"ping-pong"]
J.Chem.Educ. 62, 507 (1985). 72, 894 (1995). Kurier Chemiczny.
(1991), Nr 3, str. 12. [Metoda algebraiczna]
J.Chem.Educ. 73, 507 (1996). 74, 1367, 1368 (1997). [Równanie
Stouta, równanie Blakleya]
J.Chem.Educ. 54, 704 (1977). 59, 728 (1982). 69, 279 (1992). 71,
295 (1994). 74, 1369 (1997). [Rachunek macierzowy, programy komputerowe]
J.Chem.Educ. 26, 103 (1949). 34, 47 (1957). 39, A307 (1962). Kurier
Chemiczny. (1991), Nr 3, str. 14. J.Am.Chem.Soc. 70, 1640 (1938).
Roczniki Chemji. 135, (1921). [Dyskusja
warunków reakcji MnO4- + H2O2]
T.Pluciński. "Doświadczenia chemiczne". Wyd.
Adamantan, Warszawa 1997, s. 204, 206 i 125. [Doświadczenia z układami: MnO4-
+ H2O2 i CH2O + H2O2 oraz elektrolizą H2O2]
J.Chem.Educ., 69, 754 (1992). [Reakcje oscylacyjne tiosiarczanu z
nadtlenkiem wodoru w reaktorze przepływowym]
A.Galska-Krajewska, K.M.Pazdro."Dydaktyka chemii". PWN, Warszawa 1990, s. 368.
[O stopniach utlenienia i definicji reakcji redoks]
Chemia w Szkole. 197 (1983). [O roli intuicji chemicznej]
Tomasz Pluciński tomek@chemik.chem.univ.gda.pl
Praca wpłynęła do ChemFana: 1999-10-08
